Przeliczanie systemu binarnego na dziesiętny to umiejętność, która jest niezwykle przydatna w świecie technologii i informatyki. W prostych słowach, system binarny składa się tylko z dwóch cyfr: 0 i 1, podczas gdy system dziesiętny, którym posługujemy się na co dzień, oparty jest na dziesięciu cyfrach od 0 do 9. Aby skutecznie przeliczać liczby z jednego systemu do drugiego, należy zrozumieć, jak działają te systemy oraz jakie metody można zastosować do konwersji.
W artykule przedstawimy łatwe metody przeliczania liczb binarnych na dziesiętne oraz odwrotnie. Omówimy zarówno podstawowe zasady, jak i bardziej zaawansowane techniki, takie jak użycie funkcji w programowaniu. Dzięki temu, niezależnie od poziomu zaawansowania, każdy będzie mógł zrozumieć, jak przeprowadzać te konwersje w praktyce.
Kluczowe informacje:- Aby przeliczyć liczbę binarną na dziesiętną, mnożymy każdą cyfrę przez wagę jej pozycji i sumujemy te wartości.
- Alternatywną metodą jest dzielenie liczby przez 2, gdzie reszty zapisujemy w odpowiednich polach.
- W programowaniu można wykorzystać funkcje takie jak "strtol" i "itoa" do konwersji między systemami.
- W przypadku liczb ułamkowych, wartość części ułamkowej traktuje się chwilowo jak liczbę całkowitą.
- Przy konwersji mogą wystąpić błędy zaokrąglenia, co warto mieć na uwadze.
Jak przeliczać liczby binarne na dziesiętne - krok po kroku
Przeliczanie liczb z systemu binarnego na dziesiętny to umiejętność, która jest niezbędna w wielu dziedzinach technologii i informatyki. System binarny, składający się jedynie z cyfr 0 i 1, jest podstawą działania komputerów, podczas gdy system dziesiętny, którym posługujemy się na co dzień, oparty jest na dziesięciu cyfrach. Aby skutecznie przeprowadzić konwersję, należy zrozumieć, jak działają te systemy oraz jakie metody można zastosować do przeliczenia liczb.
W tej sekcji omówimy krok po kroku, jak przeliczyć liczby binarne na dziesiętne. Kluczowym elementem tego procesu jest pomnożenie każdej cyfry binarnej przez wagę jej pozycji, a następnie zsumowanie tych wartości. Przykładem może być liczba binarna 1010, która przelicza się na dziesiętną w następujący sposób: 1 * 2^3 + 0 * 2^2 + 1 * 2^1 + 0 * 2^0, co daje wynik 10.
Zrozumienie podstaw systemu binarnego i dziesiętnego
System binarny (podstawa 2) używa tylko dwóch cyfr: 0 i 1. Jest to system, w którym każda pozycja ma wartość będącą potęgą liczby 2. Z kolei system dziesiętny (podstawa 10) używa dziesięciu cyfr od 0 do 9. Każda pozycja w systemie dziesiętnym ma wartość będącą potęgą liczby 10. Zrozumienie tych podstaw jest kluczowe dla skutecznego przeliczania między tymi systemami.
Przykład konwersji liczby binarnej na dziesiętną
Rozważmy konkretny przykład konwersji liczby binarnej 1010 na system dziesiętny. Aby przeliczyć tę liczbę, wykonujemy następujące obliczenia: 1 * 2^3 (co daje 8) + 0 * 2^2 (co daje 0) + 1 * 2^1 (co daje 2) + 0 * 2^0 (co daje 0). Suma tych wartości wynosi 8 + 0 + 2 + 0 = 10. W ten sposób liczba binarna 1010 odpowiada liczbie dziesiętnej 10.
- Każda cyfra binarna jest mnożona przez wagę jej pozycji, co odpowiada potędze liczby 2.
- Wartości są następnie sumowane, aby uzyskać wynik w systemie dziesiętnym.
- Przykład 1010 ilustruje, jak działa ten proces.
Alternatywne metody przeliczania systemu binarnego
Istnieje wiele alternatywnych metod przeliczania liczb binarnych na dziesiętne, które mogą być bardziej efektywne w różnych sytuacjach. Jednym z najpopularniejszych sposobów jest dzielenie przez 2, które pozwala na konwersję liczb dziesiętnych na binarne. Metoda ta opiera się na dzieleniu liczby przez 2 i rejestrowaniu reszt, które są następnie odczytywane w odwrotnej kolejności. Dzięki temu można łatwo uzyskać reprezentację binarną liczby dziesiętnej.
Inną metodą jest wykorzystanie funkcji programistycznych, które automatyzują proces konwersji. W językach programowania, takich jak Python czy JavaScript, dostępne są wbudowane funkcje, które umożliwiają szybkie i efektywne przeliczanie liczb między systemami. Użycie tych funkcji znacznie ułatwia pracę, szczególnie w przypadku dużych zbiorów danych, gdzie ręczne przeliczanie byłoby czasochłonne i podatne na błędy.
| Metoda | Zalety | Wady |
|---|---|---|
| Dzielenie przez 2 | Prosta do zrozumienia i zastosowania | Może być czasochłonna dla dużych liczb |
| Funkcje programistyczne | Szybka i efektywna konwersja | Wymaga znajomości programowania |
Użycie dzielenia przez 2 w konwersji binarnej
Metoda dzielenia przez 2 polega na dzieleniu liczby dziesiętnej przez 2, a następnie zapisywaniu reszt. Proces ten powtarza się, aż do momentu, gdy liczba osiągnie 0. Na przykład, aby przeliczyć liczbę dziesiętną 18 na system binarny, wykonujemy następujące operacje: 18 ÷ 2 = 9, reszta 0; 9 ÷ 2 = 4, reszta 1; 4 ÷ 2 = 2, reszta 0; 2 ÷ 2 = 1, reszta 0; 1 ÷ 2 = 0, reszta 1. Odczytując reszty od dołu do góry, otrzymujemy wynik 10010.
Zastosowanie funkcji w programowaniu do konwersji
W programowaniu można wykorzystać funkcje, takie jak bin() w Pythonie, do konwersji liczb dziesiętnych na binarne. Na przykład, używając kodu bin(18), otrzymujemy wynik '0b10010', co oznacza, że liczba dziesiętna 18 w systemie binarnym to 10010. W JavaScript można użyć metody toString(2), co również pozwala na szybkie uzyskanie reprezentacji binarnej. Te funkcje są niezwykle przydatne, gdy potrzebujemy konwertować wiele liczb jednocześnie.
Czytaj więcej: Jak zastosować system binarny w praktyce w codziennym życiu?
Częste błędy podczas przeliczania systemu binarnego
Podczas przeliczania liczb z systemu binarnego na dziesiętny, często pojawiają się błędy, które mogą prowadzić do nieprawidłowych wyników. Jednym z najczęstszych błędów jest niewłaściwe obliczanie wag pozycji. Każda cyfra w systemie binarnym ma swoją wagę, która jest potęgą liczby 2. Jeśli użytkownik pomyli się w obliczeniach lub nie uwzględni wszystkich cyfr, wynik konwersji będzie błędny.
Innym powszechnym problemem jest zapominanie o zerach w końcowych pozycjach liczby binarnej. Na przykład, liczba binarna 1001 powinna być przeliczana jako 1 * 2^3 + 0 * 2^2 + 0 * 2^1 + 1 * 2^0. Jeśli ktoś zignoruje zera, wynik będzie zafałszowany. Aby uniknąć tych błędów, warto regularnie sprawdzać swoje obliczenia i stosować metodę podwójnej kontroli.
Problemy z zaokrągleniami w konwersji liczb
Podczas konwersji liczb dziesiętnych na binarne, szczególnie w przypadku liczb ułamkowych, mogą wystąpić problemy z zaokrągleniami. Niektóre liczby dziesiętne nie mają dokładnego odpowiednika w systemie binarnym, co prowadzi do utraty precyzji. Na przykład liczba 0.1 w systemie dziesiętnym nie może być dokładnie przedstawiona w systemie binarnym, co skutkuje błędami zaokrąglenia.
Te błędy mogą mieć poważne konsekwencje, zwłaszcza w aplikacjach wymagających wysokiej precyzji, takich jak obliczenia finansowe czy inżynieryjne. Dlatego ważne jest, aby być świadomym tych ograniczeń i stosować odpowiednie metody, takie jak zaokrąglanie do określonej liczby miejsc po przecinku, aby zminimalizować wpływ tych błędów na końcowe wyniki.
Jak unikać typowych pułapek przy przeliczaniu
Aby skutecznie unikać typowych pułapek podczas przeliczania liczb z systemu binarnego na dziesiętny, warto zastosować kilka praktycznych strategii. Po pierwsze, zawsze upewnij się, że dokładnie rozumiesz wartości wag pozycji, które przypisujesz każdej cyfrze binarnej. Niezrozumienie tego aspektu może prowadzić do błędnych wyników. Dobrą praktyką jest także pisanie obliczeń na papierze, co pozwala na lepsze śledzenie każdego kroku procesu przeliczania.
Kolejnym sposobem na uniknięcie błędów jest podwójna kontrola swoich obliczeń. Po zakończeniu konwersji warto jeszcze raz przeanalizować, czy każda cyfra została prawidłowo przeliczona, a także czy sumy zostały poprawnie obliczone. Można również korzystać z narzędzi online lub aplikacji, które automatyzują proces konwersji, co dodatkowo zmniejsza ryzyko błędów.
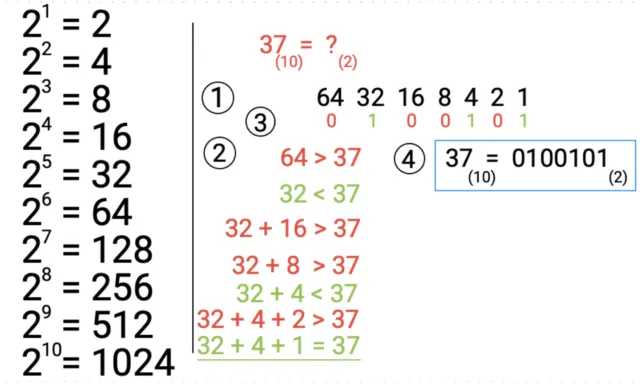
Wizualne pomoce w przeliczaniu systemu binarnego
Wizualne pomoce, takie jak tabele i diagramy, mogą znacznie ułatwić zrozumienie procesu przeliczania liczb z systemu binarnego na dziesiętny. Dzięki nim, użytkownicy mogą szybko zobaczyć, jak poszczególne cyfry wpływają na końcowy wynik. Tabele konwersji mogą zawierać przykłady, które ilustrują, jak różne liczby binarne są reprezentowane w systemie dziesiętnym, co ułatwia naukę i zapamiętywanie.
Przykładowo, tabela konwersji może zawierać liczby binarne od 0000 do 1111 oraz ich odpowiedniki w systemie dziesiętnym. Wizualizacje pomagają także w zrozumieniu, jak zmieniają się wartości w zależności od pozycji cyfry. Użycie diagramów, które pokazują proces konwersji krok po kroku, może być również bardzo pomocne, szczególnie dla osób, które dopiero zaczynają swoją przygodę z tematyką konwersji systemów liczbowych.
| Liczba binarna | Liczba dziesiętna |
|---|---|
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 2 |
| 0011 | 3 |
| 0100 | 4 |
| 0101 | 5 |
| 0110 | 6 |
| 0111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | 10 |
| 1011 | 11 |
| 1100 | 12 |
| 1101 | 13 |
| 1110 | 14 |
| 1111 | 15 |
Tabele konwersji i diagramy dla lepszego zrozumienia
Wizualne pomoce, takie jak tabele konwersji i diagramy, są niezwykle pomocne w procesie przeliczania liczb z systemu binarnego na dziesiętny. Tabele te przedstawiają liczby binarne oraz ich odpowiedniki w systemie dziesiętnym, co ułatwia szybkie odnalezienie wartości i zrozumienie relacji między tymi systemami. Użycie diagramów, które pokazują proces konwersji krok po kroku, również wspiera naukę i pomaga w zapamiętywaniu zasad konwersji.
Warto korzystać z takich wizualnych narzędzi, ponieważ pozwalają one na lepsze zrozumienie, jak poszczególne cyfry w systemie binarnym wpływają na końcowy wynik w systemie dziesiętnym. Dzięki nim, osoby uczące się konwersji mogą łatwiej przyswoić sobie zasady działania obu systemów liczbowych.
Przykłady wizualne konwersji dla różnych liczb
Przykłady wizualne konwersji liczb mogą być bardzo pomocne w zrozumieniu procesu. Na przykład, liczba binarna 1101 przelicza się na dziesiętną jako 1 * 2^3 + 1 * 2^2 + 0 * 2^1 + 1 * 2^0, co daje wynik 13. Inny przykład to liczba binarna 1010, która odpowiada liczbie dziesiętnej 10. Wizualizacje tych konwersji, takie jak diagramy pokazujące każdy krok obliczeń, mogą być użyteczne dla osób, które preferują naukę poprzez obraz.
| Liczba binarna | Liczba dziesiętna |
|---|---|
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 2 |
| 0011 | 3 |
| 0100 | 4 |
| 0101 | 5 |
| 0110 | 6 |
| 0111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | 10 |
| 1011 | 11 |
| 1100 | 12 |
| 1101 | 13 |
| 1110 | 14 |
| 1111 | 15 |
Jak wykorzystać konwersję binarną w programowaniu i technologii
W dzisiejszym świecie technologii, umiejętność przeliczania liczb z systemu binarnego na dziesiętny oraz odwrotnie ma kluczowe znaczenie w programowaniu i inżynierii oprogramowania. Przykładowo, w programowaniu niskopoziomowym, gdzie operacje na bitach są niezbędne, znajomość konwersji pozwala programistom na efektywne manipulowanie danymi. Używając języków takich jak C czy C++, programiści mogą pisać funkcje, które automatyzują te konwersje, co znacznie przyspiesza proces tworzenia oprogramowania.
Dodatkowo, w kontekście uczenia maszynowego i sztucznej inteligencji, zrozumienie, jak liczby binarne reprezentują dane, jest niezbędne do efektywnego przetwarzania informacji. W miarę jak technologia się rozwija, umiejętność pracy z różnymi systemami liczbowymi stanie się jeszcze bardziej istotna, zwłaszcza w kontekście analizy danych i przetwarzania sygnałów. Dlatego warto rozwijać te umiejętności, aby być na bieżąco z nowymi trendami i technologiami w branży.
