Dodawanie liczb w systemie binarnym to umiejętność, która jest niezwykle ważna w informatyce i elektronice. W przeciwieństwie do systemu dziesiętnego, w którym używamy cyfr od 0 do 9, w systemie binarnym operujemy jedynie na dwóch cyfrach: 0 i 1. Zrozumienie zasad dodawania w systemie binarnym jest kluczowe, ponieważ to właśnie na tych podstawach opiera się działanie komputerów oraz innych urządzeń cyfrowych.
W tym artykule omówimy podstawowe zasady dodawania binarnego, przedstawimy praktyczne przykłady oraz wyjaśnimy, jak dodawanie binarne różni się od dodawania dziesiętnego. Dzięki jasnym wyjaśnieniom i ćwiczeniom, każdy będzie mógł łatwo nauczyć się tej umiejętności i zrozumieć, dlaczego jest ona tak istotna w dzisiejszym świecie technologii.
Najważniejsze informacje:- Dodawanie binarne opiera się na czterech podstawowych zasadach: 0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1, oraz 1 + 1 = 0 z przeniesieniem 1.
- Liczby binarne zapisuje się jedna pod drugą, a dodawanie zaczyna się od najbardziej prawej kolumny.
- W przypadku wyniku dwucyfrowego, zapisuje się tylko ostatnią cyfrę, a cyfrę przenosi się do następnej kolumny.
- Dodawanie binarne różni się od dodawania dziesiętnego, szczególnie w sposobie obsługi przeniesienia.
- Praktyka dodawania więcej niż dwóch liczb binarnych jest kluczowa dla zrozumienia tego procesu.
- Dodawanie binarne ma fundamentalne znaczenie w funkcjonowaniu komputerów i systemów cyfrowych.
Jak dodawać liczby w systemie binarnym - podstawowe zasady
Dodawanie liczb w systemie binarnym jest kluczowym elementem zrozumienia działania komputerów i systemów cyfrowych. W przeciwieństwie do systemu dziesiętnego, który korzysta z dziesięciu cyfr (od 0 do 9), system binarny używa tylko dwóch cyfr: 0 i 1. W tym systemie dodawanie odbywa się na podstawie prostych zasad, które są łatwe do przyswojenia. Na przykład, dodawanie 0 i 1 daje 1, a dodawanie 1 i 1 skutkuje 0 z przeniesieniem 1 do następnej kolumny.
Ważne jest, aby zrozumieć, jak zapisywać liczby binarne przed ich dodawaniem. Liczby powinny być ustawione jedna pod drugą, tak aby cyfry o tej samej wadze znajdowały się w tej samej kolumnie. Dodawanie zaczyna się od najbardziej prawej kolumny, a jeśli wynik dodawania w danej kolumnie jest liczbą dwucyfrową, zapisywana jest tylko ostatnia cyfra, a cyfrę przenosi się do następnej kolumny. Przykład dodawania dwóch liczb binarnych, 1010 i 1101, daje wynik 10111, co odpowiada liczbie 23 w systemie dziesiętnym.
Zasady dodawania w systemie binarnym - zrozumienie podstaw
Podstawowe zasady dodawania w systemie binarnym opierają się na czterech regułach. Po pierwsze, 0 + 0 = 0. Po drugie, 0 + 1 = 1, a także 1 + 0 = 1. Ostatnia zasada, 1 + 1, daje wynik 0 z przeniesieniem 1 do kolejnej kolumny. Ważne jest, aby pamiętać, że przeniesienie działa podobnie do przeniesienia w systemie dziesiętnym, ale z uwagi na różnice w podstawie systemu, zasady te są uproszczone.
Przykłady prostych działań w systemie binarnym - krok po kroku
Aby lepiej zrozumieć, jak dodawać liczby w systemie binarnym, warto przeanalizować kilka prostych przykładów. Zacznijmy od dodawania dwóch liczb binarnych: 1010 i 1101. Aby wykonać to działanie, zapisujemy liczby jedna pod drugą, a następnie dodajemy je kolumna po kolumnie, zaczynając od prawej. W pierwszej kolumnie mamy 0 + 1, co daje 1. W drugiej kolumnie 1 + 0 również daje 1. W trzeciej kolumnie 0 + 1 znowu daje 1. W ostatniej kolumnie dodajemy 1 + 1, co daje 0 z przeniesieniem 1 do następnej kolumny.
Przeniesienie 1 do kolejnej kolumny oznacza, że dodajemy 1 do sumy w tej kolumnie. W rezultacie, w tej kolumnie mamy 1 + 0, co daje 1. Ostatecznie, suma 1010 i 1101 to 10111. Możemy to zweryfikować, przeliczając wynik na system dziesiętny: 10111 w systemie binarnym odpowiada liczbie 23 w systemie dziesiętnym. Przykład ten pokazuje, jak dodawanie w systemie binarnym różni się od dodawania w systemie dziesiętnym, ale zasady są proste i łatwe do przyswojenia.
| Liczba binarna | Wartość dziesiętna |
|---|---|
| 1010 | 10 |
| 1101 | 13 |
| 10111 | 23 |
Kluczowe różnice między systemami - co warto wiedzieć
Dodawanie w systemie binarnym różni się od dodawania w systemie dziesiętnym głównie ze względu na podstawę, na której opierają się te systemy. System binarny jest systemem o podstawie 2, co oznacza, że używa tylko dwóch cyfr: 0 i 1. Z kolei system dziesiętny, który jest powszechnie stosowany w codziennym życiu, ma podstawę 10 i korzysta z cyfr od 0 do 9. Ta różnica w podstawie wpływa na sposób, w jaki wykonujemy operacje arytmetyczne, w tym dodawanie.
Jak przenoszenie wpływa na dodawanie binarne - szczegóły procesu
Przenoszenie w systemie binarnym jest kluczowym elementem dodawania, który różni się od tego, co znamy z systemu dziesiętnego. Gdy dodajemy dwie cyfry binarne i otrzymujemy wynik równy 2, zapisujemy 0, a 1 przenosimy do następnej kolumny. Na przykład, w dodawaniu 1 + 1, wynik to 0 z przeniesieniem 1. To przeniesienie może wpływać na kolejne kolumny, co czyni proces dodawania bardziej złożonym, gdy dodajemy dłuższe liczby binarne.
Przenoszenie może wystąpić wielokrotnie podczas dodawania dłuższych liczb binarnych. Na przykład, w przypadku dodawania 111 (7 w systemie dziesiętnym) do 1, mamy 111 + 1 = 1000 (8 w systemie dziesiętnym). Przeniesienie 1 z ostatniej kolumny wpływa na wynik, co pokazuje, jak ważne jest zrozumienie tego procesu w kontekście dodawania binarnego.
Praktyczne przykłady dodawania binarnego - od prostych do złożonych
Dodawanie binarne może być na początku nieco mylące, ale z praktyką staje się znacznie prostsze. Zaczynając od prostych przykładów, możemy nauczyć się, jak dodawać liczby w systemie binarnym. Na przykład, dodając 1010 i 1100, zaczynamy od prawej kolumny. W pierwszej kolumnie 0 + 0 daje 0, w drugiej kolumnie 1 + 0 daje 1, w trzeciej kolumnie 0 + 1 daje 1, a w czwartej kolumnie 1 + 1 daje 0 z przeniesieniem 1. Ostatecznie, wynik to 10110, co odpowiada liczbie 22 w systemie dziesiętnym.
W miarę jak zdobywasz doświadczenie, możesz przejść do bardziej złożonych przykładów, takich jak dodawanie trzech lub więcej liczb binarnych. Na przykład, jeśli dodasz 1010, 1101 i 0110, musisz najpierw dodać pierwsze dwie liczby, a następnie dodać wynik do trzeciej liczby. Dodając 1010 i 1101, otrzymasz 10111, a następnie dodając 0110, uzyskasz 11101. W ten sposób można szybko i efektywnie dodawać wiele liczb binarnych.
Dodawanie więcej niż dwóch liczb binarnych - jak to zrobić
Aby dodać więcej niż dwie liczby binarne, najlepiej jest podzielić proces na mniejsze kroki. Najpierw dodaj pierwsze dwie liczby, zapisując wynik. Następnie dodaj wynik do kolejnej liczby, kontynuując w ten sposób, aż do dodania wszystkich liczb. Na przykład, aby dodać 1010, 1101 i 0110, najpierw dodaj 1010 i 1101, co daje 10111. Następnie dodaj 0110 do 10111, co daje 11101. W ten sposób można efektywnie dodawać wiele liczb binarnych, zachowując porządek i przejrzystość.
- 1. Zapisz liczby jedna pod drugą, aby cyfry o tej samej wadze były w tej samej kolumnie.
- 2. Dodawaj liczby od prawej do lewej, pamiętając o przenoszeniu, jeśli to konieczne.
- 3. Powtarzaj proces, aż wszystkie liczby zostaną dodane.
Rozwiązywanie zadań z dodawaniem binarnym - ćwiczenia do praktyki
Aby skutecznie nauczyć się dodawania w systemie binarnym, warto regularnie ćwiczyć. Oto kilka zadań, które pomogą w praktycznym zastosowaniu zasad dodawania binarnego. Na przykład, spróbuj dodać liczby 1011 i 1100. Rozpocznij od dodawania od prawej do lewej, pamiętając o przenoszeniu, gdy suma przekracza 1. Po obliczeniach powinieneś uzyskać wynik 10111, co odpowiada 23 w systemie dziesiętnym.
Innym ćwiczeniem może być dodanie 1110, 1011 i 0101. Najpierw dodaj 1110 i 1011, co da 11001, a następnie dodaj 0101 do wyniku, co ostatecznie da 11110. Takie zadania pomogą w utrwaleniu umiejętności dodawania w systemie binarnym i zrozumieniu, jak działa przenoszenie. Regularne ćwiczenie pozwoli na pewniejsze i szybsze wykonywanie obliczeń w przyszłości.
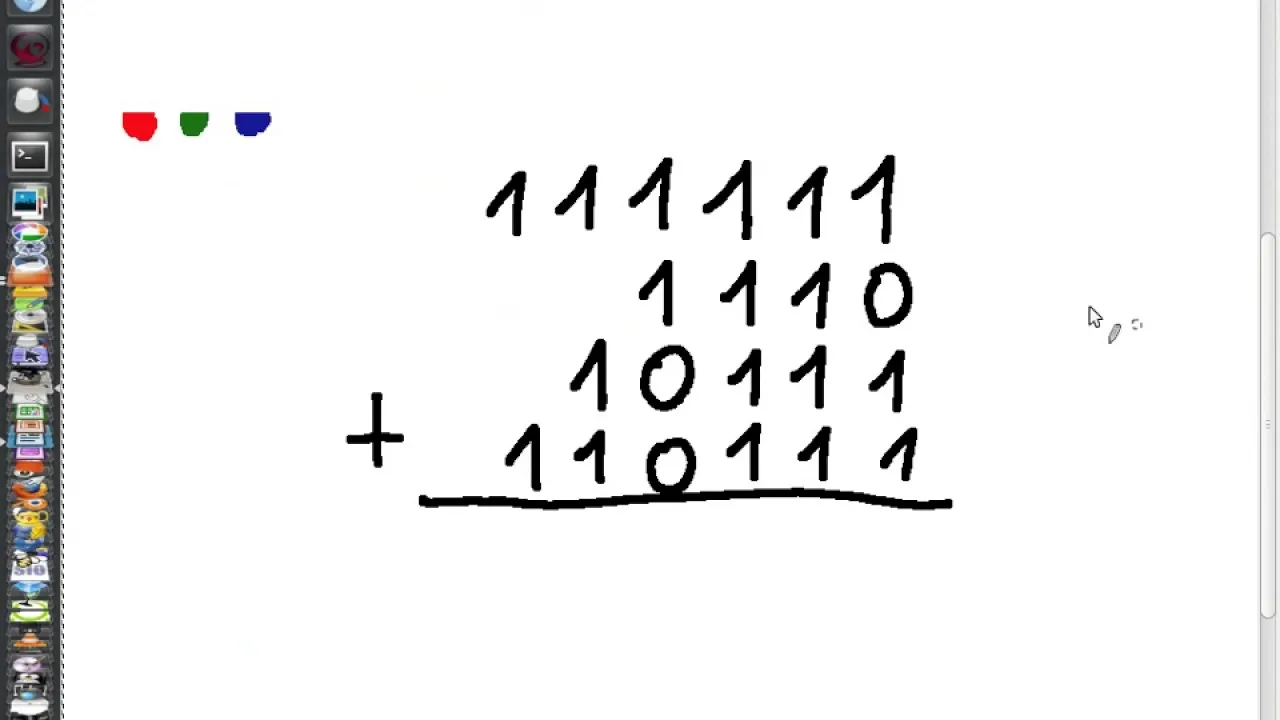
Znaczenie dodawania binarnego w informatyce - dlaczego to ważne
Dodawanie binarne jest fundamentem działania komputerów oraz systemów cyfrowych. W świecie technologii, gdzie większość danych jest reprezentowana w postaci binarnej, umiejętność dodawania liczb binarnych jest niezbędna. Komputery używają tego systemu do wykonywania obliczeń, a dodawanie binarne stanowi kluczową operację w procesach takich jak arytmetyka komputerowa, algorytmy oraz przetwarzanie danych.
Wiele nowoczesnych technologii, od prostych kalkulatorów po skomplikowane systemy operacyjne, opiera się na dodawaniu binarnym. Rozumienie tego procesu pozwala programistom i inżynierom na tworzenie bardziej efektywnych algorytmów i rozwiązań. W związku z tym, nauka dodawania w systemie binarnym jest nie tylko przydatna, ale również kluczowa dla każdego, kto chce zrozumieć podstawy informatyki i technologii komputerowej.
Jak dodawanie binarne wpływa na działanie komputerów - kluczowe aspekty
Dodawanie binarne ma bezpośredni wpływ na sposób, w jaki komputery przetwarzają informacje. Gdy komputer wykonuje operacje arytmetyczne, takie jak dodawanie, wykorzystuje algorytmy oparte na zasadach dodawania binarnego. To oznacza, że każde obliczenie, które wykonujemy na komputerze, od prostych sum po złożone obliczenia naukowe, opiera się na tym samym procesie dodawania w systemie binarnym.
| Przykład zastosowania | Opis |
|---|---|
| Operacje arytmetyczne | Podstawowe dodawanie i odejmowanie w programach komputerowych. |
| Algorytmy | Algorytmy matematyczne w programowaniu wykorzystujące dodawanie binarne. |
| Przetwarzanie danych | Analiza danych i obliczenia w bazach danych. |
Jak dodawanie binarne wpływa na rozwój sztucznej inteligencji
W miarę jak technologia staje się coraz bardziej zaawansowana, dodawanie binarne odgrywa kluczową rolę w rozwoju sztucznej inteligencji (AI). Algorytmy uczenia maszynowego, które są podstawą AI, często opierają się na operacjach arytmetycznych, w tym dodawaniu binarnym, aby przetwarzać ogromne ilości danych. W kontekście AI, umiejętność efektywnego dodawania binarnego pozwala na szybsze obliczenia, co jest niezbędne do trenowania modeli na dużych zbiorach danych.
Co więcej, zrozumienie zasad dodawania binarnego może pomóc programistom w optymalizacji algorytmów, co prowadzi do bardziej wydajnych rozwiązań w obszarze AI. W przyszłości, rozwój technologii kwantowych może wprowadzić nowe podejście do dodawania i obliczeń, gdzie zasady binarne mogą być stosowane w zupełnie nowych kontekstach. Rozwijając umiejętności w zakresie dodawania binarnego, inżynierowie i programiści mogą lepiej przygotować się na nadchodzące innowacje w dziedzinie obliczeń i sztucznej inteligencji.
