System binarny, znany również jako system dwójkowy, jest podstawowym narzędziem wykorzystywanym w technologii komputerowej. Składa się jedynie z dwóch cyfr: 0 i 1. Aby skutecznie przeprowadzać obliczenia w tym systemie, kluczowe jest zrozumienie, jak konwertować liczby między systemem binarnym a dziesiętnym oraz jak wykonywać podstawowe działania arytmetyczne, takie jak dodawanie, odejmowanie, mnożenie i dzielenie.
W artykule omówimy metody konwersji liczb dziesiętnych na binarne oraz odwrotnie, a także przedstawimy zasady wykonywania działań arytmetycznych w systemie binarnym. Dzięki tym informacjom, będziesz w stanie nie tylko przeprowadzać obliczenia, ale również unikać najczęstszych błędów, które mogą się pojawić podczas pracy z tym systemem liczbowym.
Kluczowe informacje:- System binarny składa się z cyfr 0 i 1, co czyni go fundamentalnym dla technologii komputerowej.
- Aby zamienić liczbę dziesiętną na binarną, można użyć metody potęg liczby 2 lub dzielenia przez 2 z zapisem reszt.
- Konwersja liczby binarnej na dziesiętną polega na mnożeniu każdej cyfry przez odpowiednią potęgę liczby 2.
- Podstawowe działania arytmetyczne w systemie binarnym są podobne do tych w systemie dziesiętnym, ale wymagają uwzględnienia specyfiki binarnej, jak przeniesienie czy pożyczka.
- Unikanie najczęstszych błędów przy konwersji i obliczeniach jest kluczowe dla dokładności wyników.
Jak skutecznie konwertować liczby dziesiętne na system binarny
Aby skutecznie konwertować liczby dziesiętne na system binarny, należy znać odpowiednie metody. Istnieją dwie główne techniki: metoda potęg liczby 2 oraz metoda dzielenia przez 2 z zapisem reszt. Te metody pozwalają na przekształcenie liczby dziesiętnej w odpowiadającą jej reprezentację binarną, co jest kluczowe w obliczeniach komputerowych.
W przypadku metody potęg liczby 2, zaczynamy od największej potęgi, która jest mniejsza lub równa danej liczbie dziesiętnej. Z kolei w metodzie dzielenia przez 2, liczba jest dzielona przez 2, a reszty z każdego dzielenia są zapisywane. Ostateczny wynik uzyskuje się, odczytując reszty w odwrotnej kolejności. W dalszej części artykułu omówimy szczegółowo obie metody, aby ułatwić zrozumienie tego procesu.
Metoda potęg liczby 2 dla konwersji dziesiętnej na binarną
Metoda potęg liczby 2 polega na dodawaniu odpowiednich potęg liczby 2, aby uzyskać daną liczbę dziesiętną. Na przykład, aby zamienić liczbę 9 na system binarny, należy uwzględnić potęgi liczby 2: 8 (23) i 1 (20). Ostatecznie, 9 w systemie binarnym to 1001. Wartości potęg dodajemy: 8 + 1 = 9.
Metoda dzielenia przez 2 z zapisem reszt dla konwersji
Metoda dzielenia przez 2 polega na dzieleniu liczby przez 2 i zapisywaniu reszt z każdego dzielenia. Na przykład, dla liczby 18, dzielimy ją przez 2: 18/2 = 9 (reszta 0), 9/2 = 4 (reszta 1), 4/2 = 2 (reszta 0), 2/2 = 1 (reszta 0), 1/2 = 0 (reszta 1). Ostateczny wynik odczytujemy od dołu do góry, co daje nam 10010 w systemie binarnym.
| Liczba dziesiętna | Reprezentacja binarna |
| 9 | 1001 |
| 18 | 10010 |
Jak przeliczyć liczby binarne na system dziesiętny
Konwersja liczb binarnych na system dziesiętny jest kluczowym procesem w informatyce, który pozwala na zrozumienie, jak dane są reprezentowane w komputerach. Aby przeliczyć liczbę binarną na dziesiętną, należy pomnożyć każdą cyfrę liczby binarnej przez odpowiednią potęgę liczby 2 i dodać wyniki. Proces ten wymaga znajomości pozycji każdej cyfry w liczbie binarnej, gdzie pozycja liczy się od prawej do lewej, zaczynając od zera.
Na przykład, aby przeliczyć liczbę binarną 1011 na system dziesiętny, zaczynamy od prawej strony. Mamy 1 (20), 1 (21), 0 (22), i 1 (23). Obliczamy: 1×23 + 0×22 + 1×21 + 1×20 = 8 + 0 + 2 + 1 = 11. W ten sposób, liczba binarna 1011 odpowiada liczbie dziesiętnej 11.
Obliczanie wartości dziesiętnej z liczby binarnej krok po kroku
Obliczanie wartości dziesiętnej z liczby binarnej wymaga zrozumienia potęg liczby 2. Każda cyfra w liczbie binarnej ma przypisaną potęgę, w zależności od jej pozycji. Aby to zobrazować, weźmy liczbę binarną 11010. Rozpoczynamy od prawej strony: 0 (20), 1 (21), 0 (22), 1 (23), i 1 (24). Obliczamy: 1×24 + 1×23 + 0×22 + 1×21 + 0×20 = 16 + 8 + 0 + 2 + 0 = 26. W ten sposób, liczba binarna 11010 przekształca się w 26 w systemie dziesiętnym.
- Każda cyfra binarna jest mnożona przez odpowiednią potęgę liczby 2.
- Wyniki mnożenia są sumowane, aby uzyskać wartość dziesiętną.
- Przykład: 1110 w systemie binarnym to 14 w systemie dziesiętnym.
| Liczba binarna | Liczba dziesiętna |
| 1011 | 11 |
| 11010 | 26 |
| 1110 | 14 |
Przykłady konwersji z systemu binarnego na dziesiętny
Konwersja z systemu binarnego na dziesiętny jest kluczowa w zrozumieniu, jak komputery interpretują dane. Przykładowo, liczba binarna 1101 przekształca się w systemie dziesiętnym na 13. Obliczamy to, mnożąc każdą cyfrę przez odpowiednią potęgę liczby 2: 1×23 + 1×22 + 0×21 + 1×20 = 8 + 4 + 0 + 1 = 13.
Innym przykładem jest liczba binarna 1010, która odpowiada liczbie dziesiętnej 10. Tutaj obliczenia wyglądają następująco: 1×23 + 0×22 + 1×21 + 0×20 = 8 + 0 + 2 + 0 = 10. Kolejnym przykładem jest liczba 1110, która w systemie dziesiętnym równa się 14, ponieważ 1×23 + 1×22 + 1×21 + 0×20 = 8 + 4 + 2 + 0 = 14.
- 1101 w systemie binarnym to 13 w systemie dziesiętnym.
- 1010 w systemie binarnym to 10 w systemie dziesiętnym.
- 1110 w systemie binarnym to 14 w systemie dziesiętnym.
| Liczba binarna | Liczba dziesiętna |
| 1101 | 13 |
| 1010 | 10 |
| 1110 | 14 |
Dodawanie i odejmowanie liczb w systemie binarnym bez błędów
Dodawanie i odejmowanie w systemie binarnym odbywa się na zasadzie podobnej do działań w systemie dziesiętnym, ale z uwzględnieniem specyfiki binarnej. Przy dodawaniu, jeśli suma dwóch cyfr wynosi 2 (czyli 1 + 1), zapisujemy 0 i przenosimy 1 do następnej kolumny. Na przykład, dodając 1011 (11 w systemie dziesiętnym) i 1101 (13 w systemie dziesiętnym), otrzymujemy 11000 (24 w systemie dziesiętnym). W tym przypadku, dodajemy kolumny od prawej do lewej, przenosząc wartości w razie potrzeby.
Odejmowanie w systemie binarnym również wymaga uwzględnienia przeniesienia, ale z dodatkowym elementem pożyczki. Kiedy od 0 odejmujemy 1, musimy pożyczyć 1 z następnej kolumny. Na przykład, w przypadku odejmowania 1010 (10 w systemie dziesiętnym) od 1100 (12 w systemie dziesiętnym), proces wygląda następująco: 0-0=0, 0-1 wymaga pożyczki, więc zmieniamy 1 w kolumnie wyżej na 0 i 0 w kolumnie niżej na 2 (czyli 10), co daje 10-1=1. Ostateczny wynik to 0010 (2 w systemie dziesiętnym).
Mnożenie i dzielenie w systemie binarnym z praktycznymi przykładami
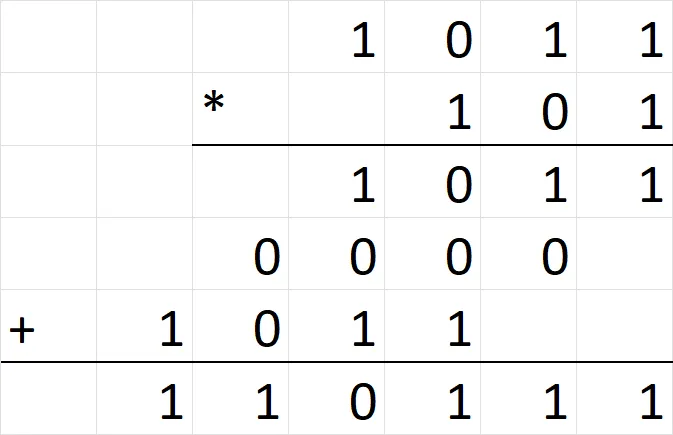
Mnożenie w systemie binarnym polega na dodawaniu przesuniętych wartości, podobnie jak w systemie dziesiętnym. Na przykład, aby pomnożyć 101 (5 w systemie dziesiętnym) przez 11 (3 w systemie dziesiętnym), wykonujemy następujące kroki: 101 x 1 = 101, a następnie przesuwamy 101 w lewo i mnożymy przez 1, co daje 1010. Dodajemy te wartości: 101 + 1010 = 1111, co odpowiada 15 w systemie dziesiętnym.
Podobnie, dzielenie w systemie binarnym polega na odejmowaniu i przesuwaniu, jak w systemie dziesiętnym. Na przykład, aby podzielić 1100 (12 w systemie dziesiętnym) przez 11 (3 w systemie dziesiętnym), zaczynamy od porównania. 11 mieści się w 110, co daje 1, a następnie przesuwamy i kontynuujemy proces. Ostatecznie, 1100 podzielone przez 11 daje 100 (4 w systemie dziesiętnym).
- Dodawanie i odejmowanie w systemie binarnym wymaga uwzględnienia przeniesienia i pożyczki.
- Mnożenie polega na dodawaniu przesuniętych wartości, a dzielenie na odejmowaniu i przesuwaniu.
- Przykłady: 101 x 11 = 1111, 1100 ÷ 11 = 100.
| Operacja | Przykład | Wynik |
| Dodawanie | 1011 + 1101 | 11000 |
| Odejmowanie | 1100 - 1010 | 0010 |
| Mnożenie | 101 x 11 | 1111 |
| Dzielenie | 1100 ÷ 11 | 100 |
Czytaj więcej: Jak dodawać w systemie binarnym - proste zasady i przykłady krok po kroku
Jak unikać najczęstszych błędów przy obliczeniach binarnych
Podczas pracy z systemem binarnym, wiele osób popełnia typowe błędy, które mogą prowadzić do nieprawidłowych wyników. Najczęstszym problemem jest nieprawidłowe dodawanie lub odejmowanie, szczególnie w sytuacjach, gdy występuje przeniesienie lub pożyczka. Na przykład, w przypadku dodawania 1 + 1, wynik powinien być 10, co może być mylące dla początkujących. Ważne jest, aby zawsze zwracać uwagę na te zasady, aby uniknąć błędów.
Innym powszechnym błędem jest nieprawidłowa konwersja między systemami liczbowymi. Użytkownicy często mylą wartości potęg liczby 2 lub pomijają pewne kroki podczas przeliczania binarnych wartości na dziesiętne. Aby uniknąć tych problemów, warto regularnie ćwiczyć konwersje i korzystać z tabel pomocniczych. Dobre zrozumienie zasad działania systemu binarnego jest kluczowe dla poprawnych obliczeń.
Najczęstsze pułapki przy konwersji między systemami liczbowymi
Podczas konwersji z systemu binarnego na dziesiętny, można napotkać różne pułapki. Jednym z najczęstszych błędów jest pomijanie potęg liczby 2 lub ich błędne obliczanie. Na przykład, przy konwersji liczby 1011, niektórzy mogą zapomnieć o dodaniu wartości dla każdej pozycji, co prowadzi do błędnych wyników. Ponadto, nieprawidłowe odczytywanie cyfr binarnych może skutkować całkowicie innymi wartościami dziesiętnymi.
Błędy w działaniach arytmetycznych i jak ich uniknąć
W działaniach arytmetycznych na liczbach binarnych, takie jak dodawanie, odejmowanie, mnożenie czy dzielenie, występują typowe błędy. Często zdarza się, że użytkownicy nie uwzględniają przeniesienia podczas dodawania lub pożyczki podczas odejmowania. Aby uniknąć tych problemów, warto regularnie ćwiczyć na konkretnych przykładach, a także korzystać z tabel, które ilustrują zasady działania w systemie binarnym. Dobre zrozumienie tych zasad pomoże w dokładniejszych obliczeniach.
Jak wykorzystać system binarny w programowaniu i technologii
Znajomość systemu binarnego ma kluczowe znaczenie nie tylko w matematyce, ale również w programowaniu i technologii. W praktyce, każdy program komputerowy opiera się na operacjach binarnych, co czyni tę wiedzę niezbędną dla programistów. Dzięki umiejętności konwersji między systemami liczbowymi, programiści mogą lepiej zrozumieć, jak działają algorytmy, a także jak optymalizować kod pod kątem wydajności. Na przykład, w językach programowania takich jak C czy Python, manipulowanie danymi w formacie binarnym pozwala na efektywniejsze zarządzanie pamięcią i szybsze przetwarzanie informacji.
W miarę jak technologia rozwija się, a systemy komputerowe stają się coraz bardziej złożone, umiejętność pracy z danymi binarnymi będzie jeszcze bardziej wartościowa. Przykładem przyszłej aplikacji jest rozwój technologii blockchain, gdzie zrozumienie binarnych operacji jest kluczowe dla analizy i tworzenia bezpiecznych transakcji. Ponadto, w kontekście sztucznej inteligencji i uczenia maszynowego, znajomość systemu binarnego może pomóc w lepszym zrozumieniu działania algorytmów oraz ich efektywności w przetwarzaniu danych. Warto więc zainwestować czas w naukę i praktykę umiejętności związanych z systemem binarnym, aby w pełni wykorzystać ich potencjał w przyszłych projektach technologicznych.
